
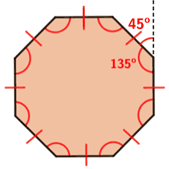
If all the sides and interior angles of an octagon are of equal measure, then it is called a regular octagon otherwise an irregular octagon. Government archives.An octagon is a closed two-dimensional figure with eight sides, eight vertices and eight interior angles. The picture is a public domain item from the U.S. Suppose you wanted a gazebo with 200 square feet of floor area. What size gazebo would to chose in order to have a minimum of 120 square feet of floor area? What length side would it have?Ĭ.

For a gazebo on size N feet, find its floor area A sq ft, and the length of a side s ft.ī. ASSUME it is the radius of the inscribed circle in other words it is the width from one side of the octagon to its opposite.Ī. Usually a web site for gazebo plans will give no indication of what the size measure is about. Octagonal gazebo plans come sizes of 6 feet to 30 feet. Suppose you were planning to construct a Gazebo with a foundation that is a regular Octagon. What is the length R of the radius of the circumscribed circle?ĩ.

The area formed by the sum of eight isosceles triangles triangles with common central angle at the center of the octagon.ħ. The area dissected into a square, rectangles, and isosceles trianglesī. What is the area of a regular octagon with a side of length a?įind at least two different approaches -Ī. Set up a right triangle and use the tangent function.Ħ. The "slice" of one-eighth of the octagon is an isosceles triangle with base of length a and height of the Apothem. The perpendicular distance from the center of a polygon to one of its sides is the Apothem. What is the length of the Apothem of a regular octagon with side of length a. twice the radius of the inscribed circle).īuild a square around the circle and construct the octagon from that.ĥ. Construct a regular octagon given the perpendicular distance from one side of the octagon to the opposite (i.e. Diagonals of the octagon would be separated by (constructable) angles of 45 degrees. the radius of the circumscribed circle).Ĭonstruct, not measure. Construct a regular octagon given the distance from the center to a vertex of the octagon (i.e. The distance from each vertex is a + x, where a is the length of the side of the octagon and x is the length of the leg of the isosceles right triangle that is "cut off" of each corner of the square, but x + a is half of the diagonal of the square.ģ. This uses the property that the external angles of a regular octagan are each 45 degrees.Ģ. Construct a regular octagon from a square of side length s.Ĭonstruct, rather than measure. Mark off lenth of two more sides of the the octagon. Bisect each right angle external to the segment.
Hint: Constuct a right angle on each end of the segment of lenght a. Construct a regular octagon given the length a of one of its sides.


 0 kommentar(er)
0 kommentar(er)
